Conectivos lógicos

Este assunto faz parte de uma série de artigos/ vídeos sobre estruturas lógicas, aqui falarei sobre conectivos lógicos.

 

Caso preferir, no vídeo abaixo tem esta postagem em áudio e vídeo

O assunto estruturas lógicas se divide em:

Proposições lógicas (lógica proposicional)

Tabela verdade

Conectivos lógicos

Tautologia, Contradição e Contingência

 

Conectivos lógicos

 

O conectivo lógico é um símbolo ou palavra que usamos para conectar duas ou mais proposições para que elas sejam válidas, de modo que a proposição composta formada dependa apenas das proposições que a originou. Por causa dos conectivos conseguimos dar um valor lógico para esta proposição formada.

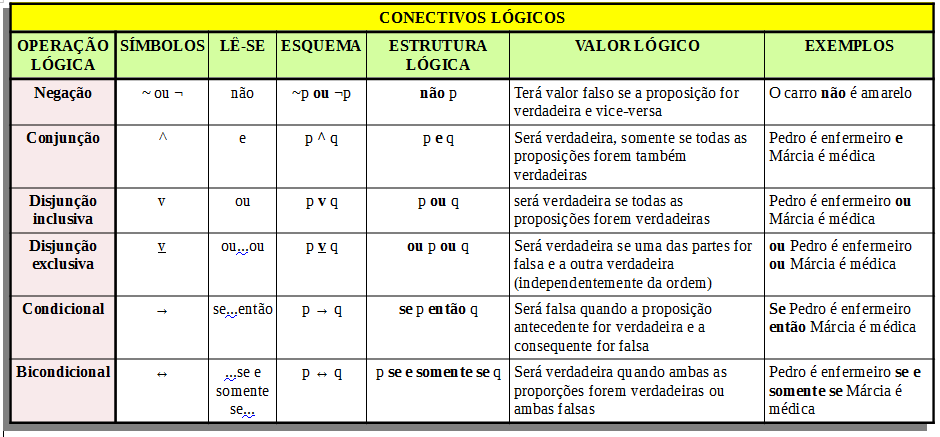
OBS.: Na tabela acima na coluna “Valor Lógico” no conceito lógico de disjunção inclusiva, o correto é: Disjunção inclusiva de uma proposição só vai ser falsa se ambas forem falsas. Se tiver uma verdadeira ou ambas verdadeiras será verdadeiro. Irei corrigir oportunamente.

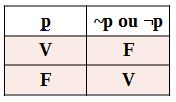
Negação (Conectivo ~ ou ¬)

 

Conectivo: “não”

Símbolo: ~ ou ¬

Esquema: ~p ou ¬p (não p)

Proposição p: O carro é amarelo

Proposição ~p: O carro não é amarelo

ou ~p : Não é verdade que o carro é amarelo

ou ~p : É falso que o carro é amarelo

 

Tabela verdade:

 

O carro é amarelo (p)

Uma proposição: 2¹ = 2

 

Conjunção (conectivo “e”)

 

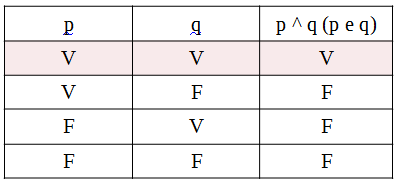
Conectivo “e” é denominado conjunção e seu símbolo é o acento circunflexo “^”

O esquema é p ^ q (p e q)

Será verdadeira somente se todas as proposições forem verdadeiras

 

Ex.:

Irei para a escola e ao teatro

p ^ q (p e q)

 

Tabela verdade:

 

Irei para a escola (p)

irei para ao teatro (q)

2 proposições = 2² = 4

A regra para conjunção é que a proposição resultante só será verdadeira se todas as proposições simples forem verdadeiras

Conectivo “ou”, denominado disjunção cujo símbolo é a letra: v ou v

 

Temos dois tipos de disjunção, a disjunção inclusiva e a disjunção exclusiva.

 

Disjunção inclusiva

 

Símbolo “v”

Conectivo “ou”

Esquema: p v q (p ou q)

 

Ex.: Como ou bebo

Embora tenha usado o conectivo ou, nada me impede de fazer as duas coisas, ou seja, significa uma inclusão.

 

Tabela verdade

Proposição 1: como

Proposição 2: bebo

Tem duas proposições: 2² = 4

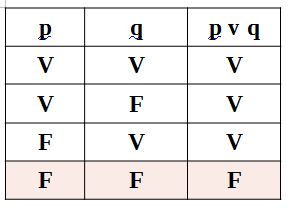
A proposição só será falsa se todas as proposições simples forem falsas

 

Disjunção exclusiva

 

Símbolo “v”

Conectivo “ou…ou”

Esquema: p v q (p ou q)

 

Ex.: Ou como ou bebo

Com a repetição do conectivo ou, ele exclui a possibilidade de fazer as duas coisas, ou seja, significa uma exclusão.

 

Tabela verdade

 

Proposição 1: Ou como

Proposição 2: Ou bebo

Tem duas proposições: 2² = 4

 

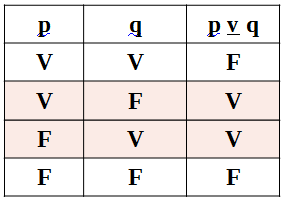
A proposição só será verdadeira se uma das proposições simples for “F” (não ocorrer) e a outra “V” (ocorrer), independentemente da ordem. Não pode acontecer “V”(ocorre) ou “F”(não ocorrer) nos dois casos, caso aconteça a proposição resultante desta operação será falsa.

 

Então, a diferença principal entre as duas disjunções é:

 

Disjunção inclusiva: Pode ocorrer uma ação ou ambas.

Disjunção exclusiva: Pode ocorrer somente uma ação.

Condicional (conectivo “se…então”)

Símbolo “→”

Conectivo “se…então”

Esquema: p → q (se p então q)

 

Ele dá uma condição para que a outra proposição exista

 

Ex.: Se nasci em Minas Gerais, então sou mineiro

Tabela verdade:

 

Proposição 1: se nasci em Minas Gerais

Proposição 2: então sou mineiro

Tem duas proposições: 2² = 4

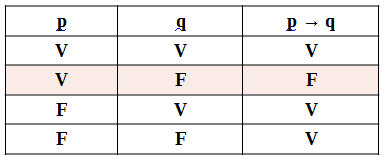
A condicional só será falsa se a proposição antecedente for verdadeira e a proposição consequente for falsa.

Bicondicional (conectivo “…se e somente se…” )

Símbolo “↔”

Conectivo “…se e somente se…”

Esquema: p ↔ q (p se somente se q)

As proposições são equivalentes, ou seja, para ser verdadeira, ambas proposições têm que ser verdadeira ou ambas tem que ser falsa.

 

Tabela verdade:

 

Proposição 1: Pedro é enfermeiro

Proposição 2: Márcia é médica

 

Lê-se: Pedro é enfermeiro se e somente se Márcia é médica

 

Tem duas proposições: 2² = 4