![]() Raciocínio lógico envolvendo problemas aritméticos, geométricos e matriciais.
Raciocínio lógico envolvendo problemas aritméticos, geométricos e matriciais.
Além dos conhecimentos de raciocínio lógico que você deve ter como tabela verdade, diagramas de Venn, conectivos, estruturas lógicas dentre outros, você deve ter conhecimento sobre aritmética (números), geometria e matrizes.
Faremos então várias questões de concurso que envolve estes conhecimentos.
Raciocínio lógico: Problemas aritméticos
Para resolver problemas aritméticos de raciocínio lógico é necessário o conhecimento de aritmética, ou seja, operações com números, ou seja, operações de adição, subtração, multiplicação, divisão, frações, múltiplos e divisores e números pares e ímpares.
QUESTÕES DE CONCURSOS
QUESTÃO 1
Ano: 2015 Banca: IDECAN Órgão: PRODEB
Sabe‐se que 100 celulares foram testados e verificou‐se que 40 aparelhos apresentavam problemas na bateria, 28 apresentavam problemas no display e 35 não apresentavam nenhum desses dois tipos de problemas. O número de aparelhos que apresentavam problemas na bateria e no display é:
A 3.
B 5.
C 7.
D 9.
SOLUÇÃO:
Número de celulares: 100
Problemas na bateria: 40
Problemas no display: 28
Celular sem problemas: 35
100 (total dos celulares) – 35 (celulares sem problema)
= 65 celulares com problema.
Vamos agora somar os celulares que tem problema:
40 (Problemas na bateria) + 28 (Problemas no display)= 68
Então,
68 (celulares com problemas) – 65 (com um ou outro problema) = 3 celulares tem os dois problemas.
RESPOSTA DA QUESTÃO 1 LETRA A
QUESTÃO 2
Ano: 2017 Banca: Quadrix Órgão: CRF – AL
Lia e Ana são amigas e suas idades são 20 e 26 anos, respectivamente. Daqui a quantos anos a soma de suas idades será igual a 100 anos?
A Em 27 anos.
B Em 34 anos.
C Em 46 anos.
D Em 54 anos.
E Em 56 anos.
SOLUÇÃO:
Primeiro somas as idades: 20 + 26 = 46
Segundo subtrai este valor de 100 = 100 – 46 = 54
Agora é só dividir o resultado por 2 = 54 / 2 = 27
RESPOSTA DA QUESTÃO 2 LETRA A
Raciocínio lógico: Problemas geométricos
Para resolver problemas geométricos de raciocínio lógico é necessário o conhecimento de geometria básica.
Caso não tenha conhecimento sobre geometria básica sugiro dar uma olhada neste artigo
QUESTÃO DE CONCURSO
QUESTÃO 1
Ano: 2017 Banca: FCC Órgão: FUNAPE
Toda a população adulta de 2.120.000 habitantes de um país será vacinada contra determinado vírus. O governo do país comprou 6 m3 da vacina. A dose de vacina é de 1,5 mL, e cada habitante adulto tem que receber duas doses. Sabendo que 1 mL corresponde à 1 cm3, no programa de vacinação de adultos descrito,
A sobrarão 120 mil doses de vacina.
B faltarão 12 mil doses de vacina.
C sobrarão 60 mil doses de vacina.
D faltarão 240 mil doses de vacina.
E faltarão 120 mil doses de vacina.
COMECE A SE PREPARAR PARA O CONCURSO DA POLÍCIA FEDERAL, CLIQUE AQUI!!
SOLUÇÃO:
População (número de pessoas a serem vacinadas) = 2.120.000 habitantes
Vacina comprada (disponível) = 6 m3
Cada dose = 1,5 ml
Cada 1 ml corresponde a 1 cm3
Habitante tem que receber duas doses = 1,5 x 2 = 3 cm3
Vamos converter a quantidade comprada para cm3:
1 m3 = 1.000.000 cm3 logo
6 m3 = 6.000.000 cm3
6.000.000 (cm3 comprado) dividido por 3 (cm3 dose por habitante) = 2.000,000
Então 2.000.000 de pessoas serão vacinadas
Logo;
2.120.000 (habitantes totais) – 2.000.000 (habitantes vacinados) = 120.000
Então faltarão 120.000 habitantes a serem vacinados
Como cada habitante recebem duas doses: 120.000 x 2 = 240.000
Faltarão então 240.000 doses da vacina para atender a todos
RESPOSTA LETRA D
Raciocínio lógico: Problemas matriciais
Para resolver problemas matriciais de raciocínio lógico é necessário o conhecimento de matrizes.
Caso não tenha conhecimento sobre matrizes sugiro dar uma olhada neste artigo
Matrizes, determinantes e sistemas lineares
QUESTÕES DE CONCURSOS
QUESTÃO 1
Ano: 2010 Banca: UFMT Órgão: Prefeitura de Cuiabá – MT
Em cada um dos quatro dias de desfile de carnaval, a temperatura foi medida em graus Celsius, no meio da multidão, em três momentos distintos. Cada elemento aij da matriz A abaixo corresponde à medida da temperatura no momento i do dia j.
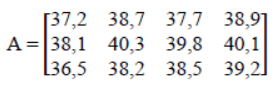
Qual foi, respectivamente, o momento e o dia em que se registrou a maior temperatura durante os desfiles?
A 2.º e 4.º
B 2.º e 2.º
C 3.º e 2.º
D 3.º e 4.º
SOLUÇÃO
Maior temperatura é 40,3 que fica na linha 2 e coluna 2 a2×2
RESPOSTA DA QUESTÃO 1 LETRA B
QUESTÃO 2
Ano: 2014 Banca: IDECAN Órgão: Prefeitura de Ubatuba – SP
Uma rádio apresenta dois programas com músicas antigas das décadas de 60, 70 e 80, cujos números de músicas de cada década são sempre iguais conforme indicado a seguir: ⚫ Programa A: cinco canções da década de 60, três da década de 70 e quatro da década de 80; e, ⚫ Programa B: oito canções da década de 60, duas da década de 70 e sete da década de 80. Considere que nos dois primeiros meses a partir das estreias desses programas os mesmos foram apresentados várias vezes: ⚫ 1º mês: 50 programas A e 20 programas B; e, ⚫ 2º mês: 30 programas A e 40 programas B. A matriz que representa a quantidade de músicas exibidas nos dois meses considerados é
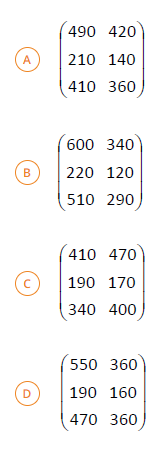
SOLUÇÃO:
ENUNCIADO: Uma rádio apresenta dois programas com músicas antigas das décadas de 60, 70 e 80, cujos números de músicas de cada década são sempre iguais conforme indicado a seguir:
Programa A: cinco canções da década de 60, três da década de 70 e quatro da década de 80;
Programa B: oito canções da década de 60, duas da década de 70 e sete da década de 80.
Montando uma matriz:

Considere que nos dois primeiros meses a partir das estreias desses programas os mesmos foram apresentados várias vezes:
1º mês: 50 programas A e 20 programas B; e,
2º mês: 30 programas A e 40 programas B.
Montando agora outra matriz:
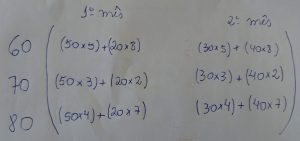
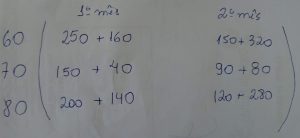

RESPOSTA DA QUESTÃO 2 LETRA C


