![]() Grandezas diretamente proporcionais e grandezas inversamente proporcionais
Grandezas diretamente proporcionais e grandezas inversamente proporcionais
Grandezas são tudo que pode ser medido como comprimento, volume, capacidade, tempo, massa, temperatura, velocidade, idade, área dentre outras.
No vídeo abaixo eu resolvo várias questões.
Grandezas diretamente proporcionais:
Como o próprio nome diz, são diretamente proporcionais, ou seja, elas crescem juntas ou diminuem juntas. Devem variar na mesma razão (proporção).
Ex.: Se um trem percorre 80 km em 1 hora ele em 2 horas percorrerá 160 km. Se percorrer 320 km terá gasto 4 horas.
A quilometragem (distância) é diretamente proporcional ao tempo.
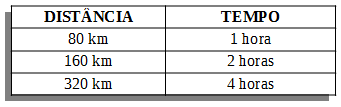
Dobrando o tempo se percorre o dobro de distância (diretamente proporcional)
Sempre tem uma grandeza proporcional à outra.
Grandeza inversamente proporcional:
Como o próprio nome diz, são inversamente proporcionais, ou seja, quando uma cresce a outra diminui e quando uma diminui a outra cresce. Variam em razão inversa.
Ex.: Se um trem que sai de uma cidade em uma velocidade de 50 km/h leva 3 horas para chegar na próxima cidade, então se ele dobrar de velocidade, ou seja, 100 km/ hora ele levará 1,5 para chegar na mesma cidade. Se a velocidade dobrar novamente (200 km/h) o tempo cai pela metade 0,75 horas
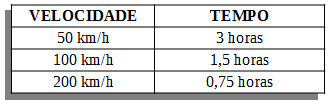
Dobrando a velocidade, cai pela metade o tempo (inversamente proporcionais)
Vemos que são grandezas inversamente proporcionais, ou seja, quando mais aumenta a velocidade, mais diminui o tempo de viagem.
Para calcular proporções normalmente se usa a regra de três e a constante de proporcionalidade k
ATENÇÃO:
Quando a questão fala em proporcionalidade, nós devemos utilizar a constante de proporcionalidade k na seguinte forma:
Grandeza diretamente proporcional: multiplicamos os valores pela constante k.
Grandeza inversamente proporcional: dividimos a constante k pelos valores dados.
E na regra de três simples quando for diretamente proporcional multiplica as diagonais e na inversamente proporcional inverte uma coluna ou multiplica-se as horizontais.
Na resolução de questões, você entenderá melhor e verá que é muito simples.
Questões de concursos
QUESTÃO 1 (questão de grandeza diretamente proporcional)
Ano: 2020 Banca: IBADE Órgão: IBGE – IBGE – Recenseador
Fernanda e Daniel jogaram juntos na loteria e acertaram cinco números, gerando um prêmio de R$ 750.000,00. Fernanda investiu R$ 80,00 e Daniel R$ 70,00 sobre o total do valor apostado, por isso o prêmio foi dividido em partes diretamente proporcionais à participação de cada um na aposta.
Qual a parte que coube a Daniel?
A R$300.000,00
B R$315.000,00
C R$325.000,00
D R$330.000,00
E R$350.000,00
RESOLUÇÃO:
Prêmio: 750.000,00
Fernanda investiu R$ 80,00
Daniel investiu Daniel R$ 70,00
Prêmio dividido diretamente proporcional ao que investiram
Ele pergunta: Qual a parte que coube a Daniel?
Vamos achar a constante de proporcionalidade k
Fernanda Daniel Prêmio
80 70 750.000
1º Vamos calcular a constante de proporcionalidade k montando uma equação:
Grandeza diretamente proporcional: multiplicamos os valores pela constante k.
Fernanda Daniel Prêmio
80k + 70k = 750.000
80k + 70k = 750.000
150k = 750.000 → k = 750.000/150 →k = 5.000
Ele pergunta: Qual a parte que coube a Daniel?
Daniel = 70k → 70 x 5.000 = 350.000
RESPOSTA DA QUESTÃO 1 LETRA E
QUESTÃO 2 (questão de grandeza indiretamente proporcional)
Ano: 2020 Banca: OBJETIVA Órgão: Prefeitura de Califórnia – PR
Uma caixa de chocolate contém 36 chocolates. Deseja-se distribuir esses chocolates de maneira inversamente proporcional à idade de três irmãos, que possuem 6, 8 e 12 anos. Sendo assim, assinalar a alternativa que apresenta a quantidade de chocolates que o irmão de 6 anos recebeu:
A 18
B 16
C 12
D 8
RESOLUÇÃO:
Caixa = 36 chocolates
Vai ser dividido inversamente proporcional entre os 3 irmãos de 6, 8, e 12 anos.
A questão pergunta quanto recebeu o irmão de 6 anos.
Será distribuído inversamente proporcional, ou seja, o que tem menos idade receberá mais.
Nesta questão utilizaremos a constante de proporcionalidade.
A B C
6 8 12
1º Vamos calcular a constante de proporcionalidade k montando uma equação:
Grandeza inversamente proporcional: dividimos a constante k pelos valores dados.
A B C

mmc de 6,8,12 = 24

Agora é calcular quanto cada um ganhou:
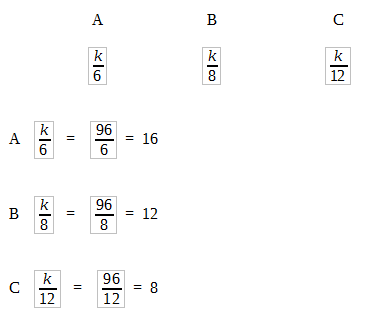
Ele pergunta quantos chocolates o irmão de 6 anos recebeu:
Ele recebeu 16 chocolates
RESPOSTA DA QUESTÃO 2 LETRA B
QUESTÃO 3
Ano: 2020 Banca: Itame Órgão: Prefeitura de Edéia – GO
Dois advogados deverão analisar 45 processos, e resolveram dividir essa quantidade em partes inversamente proporcional ao respectivo tempo de trabalho de ambos na empresa. Se o primeiro que trabalha na empresa há 28 anos analisar 25 dos processos. Quantos anos de trabalho o segundo tem na empresa?
A 32
B 33
C 34
D 35
RESOLUÇÃO:
Número de processos: 45
O advogado A de 28 anos de trabalho e analisou 25 processos
Então:
O advogado B que não sabemos o tempo dele de trabalho analisou 20 processos →45 – 25 = 20
A questão quer saber que eles resolveram dividir essa quantidade em partes inversamente proporcional ao respectivo tempo de trabalho de ambos na empresa.
É só montar uma regra de três simples:
Tempo de trabalho Processos
28 25
X 20
Agora atenção se fosse diretamente proporcional você multiplicaria as diagonais, mas como ele pede inversamente proporcional você multiplica as horizontais, ficando assim:
20 X = 28 x 25
![]()
Temos um segundo método que é inverter uma das colunas, que o transformaria em diretamente proporcional e assim multiplica as diagonais:
Tempo de trabalho Processos
28 25
X 20
Inverte uma das colunas transformando em diretamente proporcional:
Tempo de trabalho Processos
28 20
X 25
20 X = 28 x 25
![]()
RESPOSTA DA QUESTÃO 3 LETRA D
Você escolhe o método que melhor se adapte a você
QUESTÃO 4
Ano: 2017 Banca: FGV Órgão: IBGE – Recenseador
A quantia de 900 mil reais deve ser dividida em partes proporcionais aos números 4, 5 e 6.
A menor dessas partes corresponde a:
A 210 mil reais;
B 240 mil reais;
COMECE A SE PREPARAR PARA O CONCURSO DA POLÍCIA FEDERAL, CLIQUE AQUI!!
C 270 mil reais;
D 300 mil reais;
E 360 mil reais.
RESOLUÇÃO:
4 + 5 + 6 =15
900.000 / 15 = 60.000
A menor parte é 4 então,
60.000 x 4 = 240.000
RESPOSTA DA QUESTÃO 4 LETRA B
QUESTÃO 5
Ano: 2020 Banca: Quadrix Órgão: CFO-DF
Julgue o item.
Suponha‐se que duas grandezas sejam inversamente proporcionais. Nesse caso, se uma grandeza tiver um acréscimo de 100%, então a outra também terá um acréscimo de 100%.
Certo
Errado
COMENTÁRIO: Se são grandezas inversamente proporcionais, quando uma cresce a outra decresce.
RESPOSTA DA QUESTÃO 5 ERRADO
QUESTÃO 6
Ano: 2020 Banca: IBADE Órgão: IBGE – Recenseador
As duas sucessões numéricas a seguir são diretamente proporcionais: (8, x, y) e (12,15,21), onde x e y representam números inteiros desconhecidos. Quais os valores de x e y respectivamente?
A 10 e 12
B 12 e 14
C 12 e 16
D 10 e 14
E 14 e 16
RESOLUÇÃO:
8 ———- 12
X———–15
Y———–21
A sucessão é proporcional então vamos analisar (raciocínio lógico)
8————12 então aumentou 4 então equivale a 1/3 do valor de 12
X———–15 X + 5 (1/3 do valor de 15) = 15 → X = 15 – 5 → X = 10
Y————21 Y + 7 (1/3 do valor de 21) = 21 → y = 21 – 7 → Y = 14
RESPOSTA DA QUESTÃO 6 LETRA D
QUESTÃO 07
Ano: 2020 Banca: Quadrix Órgão: METRÔ-SP
Uma empresa paulistana decidiu premiar três funcionários que se destacaram no ano de 2019. Ela ofereceu uma quantia em dinheiro para ser dividida entre os três de forma inversamente proporcional ao número de faltas justificadas ocorridas durante aquele ano. Entre os três, o funcionário que recebeu a menor quantia, que foi igual a R$ 3.300,00, teve oito faltas justificadas no ano. Diante do exposto, pode-se dizer que o funcionário que teve apenas três faltas justificadas no ano de 2019 recebeu um total de
A R$ 1.237,50.
B R$ 5.500,00.
C R$ 7.637,50.
D R$ 8.800,00.
RESOLUÇÃO:
Menor quantia: R$ 3.300,00 e teve 8 faltas
Ele pergunta quanto receberá o funcionário que teve 3 faltas
Distribuição inversamente proporcional
Regra de três simples

QUESTÃO 8
Ano: 2020 Banca: Instituto UniFil Órgão: Prefeitura de Santo Antônio do Sudoeste – PR
Uma empresa resolveu distribuir um bônus natalino aos seus três funcionários. Para ser justo, o proprietário da empresa fez uma divisão inversamente proporcional ao número de faltas injustificáveis que cada funcionário teve durante o ano. O funcionário A teve 5 faltas injustificáveis durante o ano, o funcionário B teve 4 faltas e o funcionário C teve 6 faltas. Considerando que o valor do bônus a ser distribuído era de R$ 5.550,00, analise as alternativas e indique qual foi a diferença entre o valor recebido pelo funcionário B e o funcionário C.
A R$ 450,00
B R$ 300,00
C R$ 750,00
D R$ 650,00
RESOLUÇÃO:
Distribuição inversamente proporcional
Funcionário A: 5 faltas
Funcionário B: 4 faltas
Funcionário C: 6 faltas
Valor distribuído de R$ 5.550,00
Ele pergunta qual é a diferença entre o valor recebido pelo funcionário B e o funcionário C: B – C
A B C
5 4 6
1º Vamos calcular a constante de proporcionalidade k montando uma equação:

Agora é calcular quanto cada um ganhou:

Ele pergunta qual é a diferença entre o valor recebido pelo funcionário B e o funcionário C:
B – C = 2.250 – 1.500 = 750
RESPOSTA DA QUESTÃO 8 LETRA C
QUESTÃO 09
Ano: 2020 Banca: IBADE Órgão: Prefeitura de Santa Luzia D`Oeste – RO
Dividindo a quantia de R$ 3760,00 em 4 partes diretamente proporcionais aos números 2, 5, 6 e 7, temos como menor valor após a divisão:
A R$ 300,00
B R$ 370,00
C R$ 376,00
D R$ 940,00
E R$ 1128,00
RESOLUÇÃO:
Divisão diretamente proporcional: R$ 3760,00 em 4 partes
Números: 2, 5, 6 e 7
2 + 5 + 6 + 7 = 20 partes
Agora é só calcular quanto vale cada parte:
3.760/ 20 = 188
Então ele quer o menor valor após a divisão
2 x 188 = 376
RESPOSTA DA QUESTÃO 09 LETRA C
QUESTÃO 10
Ano: 2020 Banca: Instituto Access Órgão: Câmara de Orizânia – MG
O lucro de uma empresa será dividido de forma diretamente proporcional aos investimentos dos seus proprietários, Márcio e Amanda. Sabe-se que Márcio investiu R$ 10.000,00 e Amanda R$ 15.000,00. Coincidentemente, a empresa lucrou R$ 25.000,00 (mesmo valor do investimento). Desse modo, Amanda receberá (em reais) o seguinte valor a mais que Márcio:
A 15.000,00.
B 10.000,00.
C 5.000,00.
D 2.000,00.
E 1.500,00.
COMENTÁRIO:
Neste caso específico podemos resolver de duas maneiras:
1ª Maneira
Márcio investiu R$ 10.000,00
Amanda investiu R$ 15.000,00
Total investido R$ 25.000,00
Lucraram R$ 25.000,00
Logo se o lucro é dividido proporcionalmente ao capital investido eles receberam os mesmos valores que investiram, ou seja:
Márcio lucrou R$ 10.000,00
Amanda lucrou R$ 15.000,00
Ele quer saber quanto Amanda receberá a mais do que Márcio: 15.000 – 10.000 = 5.000,00
2ª maneira:
Achar a constante de proporcionalidade.
Se são diretamente proporcionais, multiplica-se valor.
10000k + 15000k = 250000 → 250000k = 250000 → k = 25000/ 25000 → k = 1
Então:
Márcio lucrou: 10000k = 10000 x 1 → 10000
Amanda lucrou: 15000k = 15000 x 1 → 15000
Ele quer saber quanto Amanda receberá a mais do que Márcio: 15.000 – 10.000 = 5.000,00
RESPOSTA DA QUESTÃO 10 LETRA C



Excelente página com exercícios, dou nota mil.
Oi Anderson, obrigado